python 强连通图路线查找问题

图结构在处理比较复杂的数据关联是常用到的一个数据结构，前面提到的树结构就是属于图的子集。

python官方提供的解决方案（https://www.python.org/doc/essays/graphs/）中用字典来处理图结构。  

树结构通常用来处理1对多，而图则用来处理多对多的问题，比如城市电网问题，a城市的光纤连通了b、c城市，b城市连通了a、c，c连通b、d，d连通c。 我们想知道从a到d的是否联网，如果连了，可以选择那些路线（全部路线问题），或者怎么样让光纤走最少的城市（最少节点问题），或者怎么样从a到d拉光纤最短（最短路径问题，比较复杂，下次探讨）  

可以简化成一个简单的无向图，如下

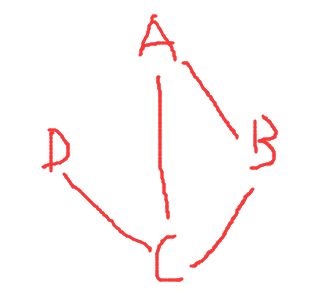
class Graph():

    #查询所有路径
    def find_all_path(self,graph_dict,start,end,path=[]):
        path = path+[start] #这里不可以用append,否则将改变path的原值，=赋值可以后path成为局部变量
        if start == end:
            return [path]
        paths = []
        if start in graph_dict:
            dict = graph_dict[start]
            for i in dict:
                if i not in path:
                    newpath = self.find_all_path(graph_dict, i, end,path)
                    if newpath:
                        paths.extend(newpath)
            return paths
        # return paths

    #查询节点最少路径 2种办法，一种直接用上面的方面，每次递归通过长度判断更小的path，递归完获取最小的
    #第二种通过队列，可以不必递归完成所有路线的判断，如下
    def find_short_path(self,graph_dict,start,end,path=[],list=[]):
        path = path + [start]
        if start == end:
            return [path]
        if start in graph_dict:
            dict = graph_dict[start]
            for i in range(len(dict)):
                list.append((path,dict[i]))
            # print(list)
            for i in list:
                if type(i)==tuple:
                    path = i[0]
                    i = i[1]
                if i not in path:
                    list.pop(0)
                    return self.find_short_path(graph_dict, i, end, path,list)


if __name__ == '__main__':
    '主函数'
    # 无权重值路线查找
    # 连通图（无向无权重值的图）
    graph_dict = {
        'a':['b','c'],
        'b':['a','c'],
        'c':['d','b'],
        'd':['c']
    }

    graph = Graph()
    start = 'a'
    end = 'c'


    print('所有路线',graph.find_all_path(graph_dict,start,end))
    print('最少节点路线',graph.find_short_path(graph_dict, start, end))

所有路线 [['a', 'b', 'c', 'd'], ['a', 'c', 'd']]
最少节点路线 [['a', 'c', 'd']]

图结构 路线问题