单源最短路径可以理解为N个城市拉电网问题,求某个点到其他所有点的拉电网最短距离问题。常见的地图导航也是同样的原理(从你的位置到目标位置有N个点互相连通,找出最短路线)。
Dijkstra最短路径算法是一种单源最短路径,针对的是非负权边。所谓单源最短路径就是指定一个出发顶点,计算从该源顶点出发到其他所有顶点的最短路径。
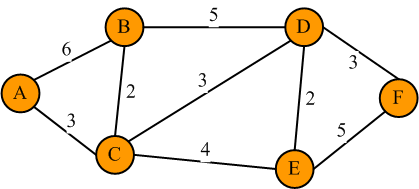
针对下图我们求从a点到其他点的最短路径和最短距离
class DisjointSet():
pass
#返回dict中值最小且不为-1 对应的键
def get_least_key(dict):
list_key = list(dict.keys())
list_value = list(dict.values())
key = 0
value = 0
for i in range(len(list_value)):
if list_value[i]!=-1:
if value==0:
key = i
value = list_value[key]
if list_value[i] < value:
value = list_value[i]
key = i
# print(key ,value)
return list_key[key]
if __name__ == '__main__':
'主函数'
# 求单源最短路线 有权重无向 无向图需要每个连线标注2次:a->b ,b->a
graph_dict = {
'a': [('b', 6), ('c', 3)],
'b': [('a', 6),('c', 2), ('d', 5)],
'c': [ ('a', 3),('b', 2),('d', 3), ('e', 4)],
'd': [('b', 5),('c', 3),('e', 2), ('f', 3)],
'e': [('c', 4),('d', 2),('f', 5)],
'f': [('d', 3), ('e', 5)],
}
# 最小生成树
start = 'a'
print('起点为:',start)
start_len = 0
start_path = ['a']
# for i,index in graph_dict.items():
# print(i)
# print(index)
old_dict_len = {
'b':-1,
'c':-1,
'd':-1,
'e':-1,
'f':-1,
}
# print(get_least_key(old_dict_len))
dict_len = {
'a':0,
}
dict_path = {
'a':['a']
}
while len(old_dict_len)>0:
for i in graph_dict[start]:
if i[0] in old_dict_len:
if old_dict_len[i[0]]==-1 or old_dict_len[i[0]]>i[1]+start_len:
old_dict_len[i[0]]=i[1]+start_len
dict_path[i[0]] = start_path+[i[0]]
start = get_least_key(old_dict_len)
dict_len[start] = old_dict_len.pop(start)
start_len = dict_len[start]
start_path = dict_path[start]
print('从起点到每个点的最短距离为:',dict_len)
print('从起点到每个点的最短路线为:',dict_path)起点为: a
从起点到每个点的最短距离为: {'a': 0, 'c': 3, 'b': 5, 'd': 6, 'e': 7, 'f': 9}
从起点到每个点的最短路线为: {'a': ['a'], 'b': ['a', 'c', 'b'], 'c': ['a', 'c'], 'd': ['a', 'c', 'd'], 'e': ['a', 'c', 'e'], 'f': ['a', 'c', 'd', 'f']}